What is Linear Regression?

• Linear regression is a fundamental algorithm in machine learning and can be thought of as simple supervised learning.
• It models the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data.

Linear Regression Equation

• When rewritten for a simple linear regression model, we write it:
  
  • : Dependent variable
  • : Independent variable
  • : Intercept
  • : Slope

Loss Function

• The goal of linear regression is to find the values of that minimize the difference between the observed and predicted values of .
• We quantify this using a loss function called Mean Squared Error (MSE), calculated as:
  
  • : Actual value
  • : Predicted value
  • : Number of observations
• All models have a loss function, to "fit" a model is to minimize the loss function.

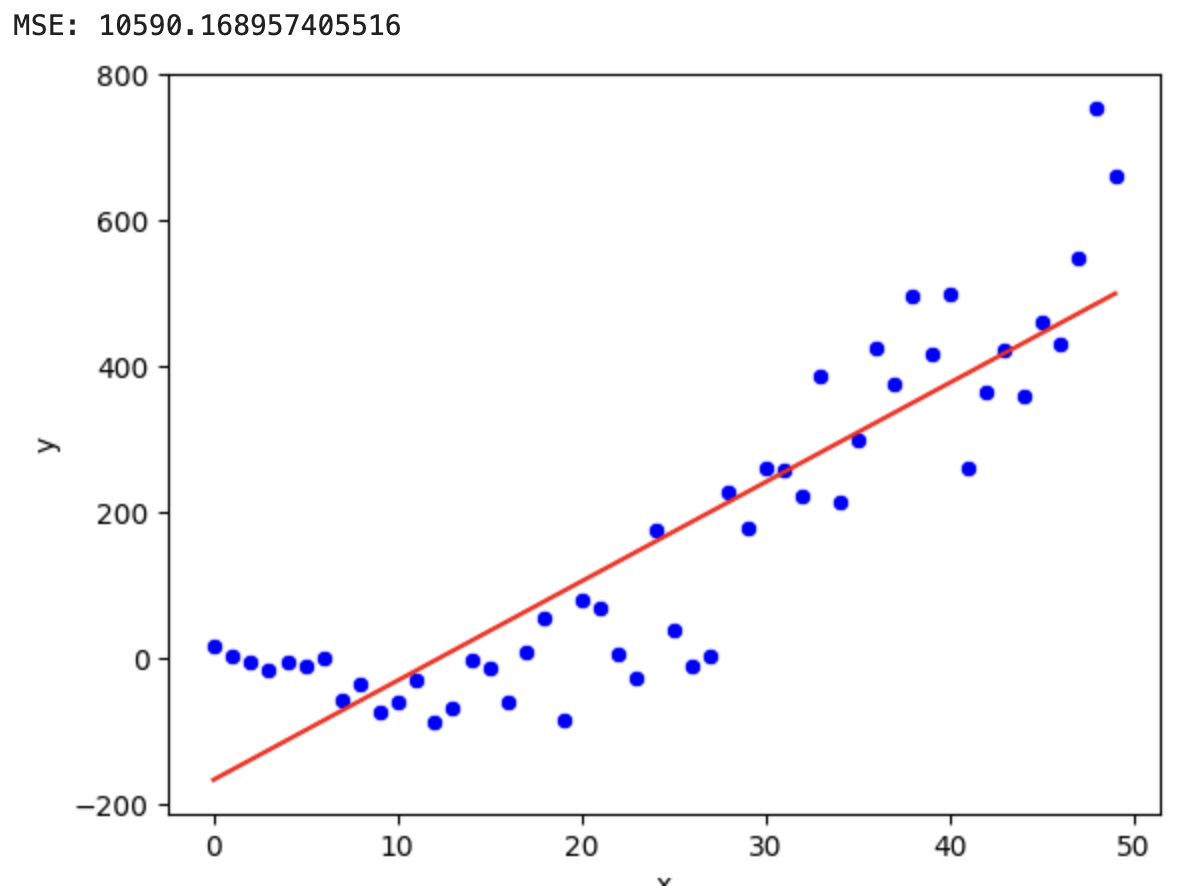
Visualizing Linear Regression

• The line of best fit minimizes the vertical distances (errors) between the observed points and the predicted line.
• The sum of these squared distances is what we aim to minimize using the loss function.

Why MSE Instead of Mean Absolute Error (MAE)?

• • MSE penalizes larger errors more than MAE.
  • Squaring the errors emphasizes larger discrepancies, making the model more sensitive to outliers.
  • MSE is differentiable, which makes it easier to optimize using gradient-based methods.

Fitting a Linear Regression

Normal Equation

• For small to medium-sized datasets, linear regression can be solved using simple matrix math:
  
  • : Matrix of input features
  • : Vector of output values
• For larger datasets (and for other algorithms we'll go over later), Gradient Descent is used.
• For this class, we'll just use SKLearn.

Multiple Linear Regression

• For multiple linear regression, the model includes multiple independent variables:
  • : Independent variables
  • : Coefficients

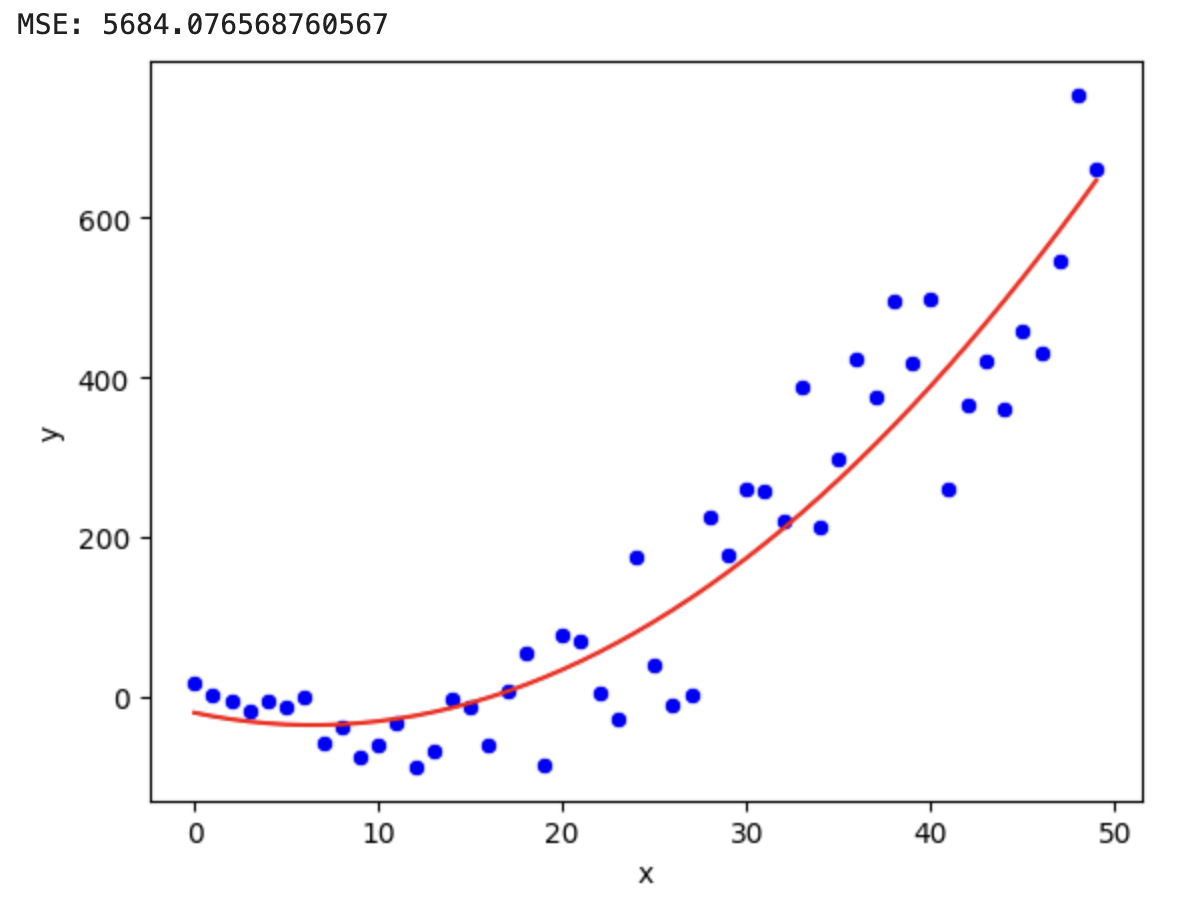
What is Polynomial Regression?

• Extension of linear regression to capture non-linear relationships.
• Fits a polynomial equation to the data

Polynomial Regression Equation

• • : Dependent variable
  • : Independent variable
  • : Coefficients

Feature Transformation

• Transform into polynomial features
• Example:
  • Original feature:
  • Polynomial features:

Model Training

• Similar to linear regression but with polynomial terms
• Minimize the sum of squared errors (SSE)
• Example:

Overfitting and Underfitting

• Underfitting: Model is too simple, misses the pattern
• Good Fit: Model captures the underlying pattern without noise
• Overfitting: Model is too complex, captures noise